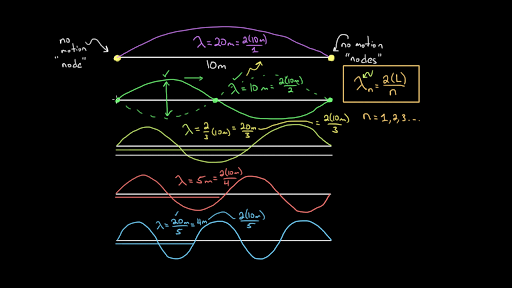
standing waves

By D Law

aka 

The Hidden

A MATHEMATICAL FORMULAE SHOWING HOW STANDING WAVES CREATE AN OUTPUT MOE THAN THE SUM OF ITS INDIVIDUAL PARTS

that’s a question with some resonance—literally.

To show mathematically how standing waves can produce an output that’s more than the sum of their individual parts, you're venturing into the realm of constructive interference—where waves align just right to amplify each other.

Here’s a simplified formulaic way to express it:

Individual Traveling Waves

Let’s say we have two waves:

y1(x,t)=Asin⁡(kx−ωt)

y2(x,t)=Asin⁡(kx+ωt)

These are identical in amplitude A, frequency ω, and wavenumber k, but traveling in opposite directions.

Standing Wave Formation

Add them together:

y(x,t)=y1(x,t)+y2(x,t)=Asin⁡(kx−ωt)+Asin⁡(kx+ωt)

Using the identity sin⁡a+sin⁡b=2sin⁡(a+b2)cos⁡(a−b2), we get:

y(x,t)=2Asin⁡(kx)cos⁡(ωt)

This is the equation of a standing wave. Notice that the amplitude has doubled from A to 2A—but power goes as amplitude squared, so:

Power ∝ Amplitude² → (2A)2=4A2

That’s four times the power of a single wave—more than the simple sum of energies.

In essence: When two coherent waves meet in just the right way, the result isn’t just A + A = 2A. It’s an entirely new pattern—a standing wave with energy density that can far exceed the individual inputs.